Last updated on April 5th, 2023 at 12:06 pm
Ratio And Proportion Problem Shortcut Tricks for Bank PO SSC Railway Exam
In quantitative aptitude, Ratio And Proportion chapter plays an important role in any competitive examination like SSC CGL, SSC CHSL, SBI PO, SBI Clerks, IBPS PO, IBPS Clerks, railways and Lic etc so I have explained basic to advanced Ratio And Proportion problem concepts, shortcut tricks, and solution which will help you scoring good marks in exam and also save your valuable time.
In Quantitative Aptitude Ratio And Proportion, concept helps to solve a problem of Data Interpretation, Profit and loss, SI, and CI, Mixture and allegations etc.In this post, I have covered introduction and the very common type of Ratio And Proportion problem that are frequently asked in the various competitive exam.
Ratio And Proportion Concept
Ratio – It is a way of comparing two numbers or quantities and showing the relationship between them.
It is denoted by → ‘:’
Ex: In a class, there are 60 boys and 40 girls. What is the ratio of boys and girls?
Sol.: boys=60 and girls=40
Ratio= boys/girls =60/40=3/2=3:2
3:2 means हर three boys पर 2 girls है | या मैं ऐसा भी बोल सकता हूँ कि 5(i.e 3+2=5) students में 3 boys है or 2 girls है|
→ If boys : girls = 3 : 2 क्या मैं ऐसा भी बोल सकता हूँ कि boys=3 or girls=2 तो मेरा Ans. है नहीं. क्योंकि मैंने common factor को cancel out कर दिया है उसके बाद हमे 3:2 प्राप्त हुआ है |
यदि हमे boys and girls का individual value निकलना हो तो common factor से multiply करना होगा |
that means boys=3×20=60 and girls=2×20=40.here common factor=20 यहाँ पर मुझे common factor मालूम था तो मैंने individual value निकाल लिया |
यदि मुझे common factor मालूम नहीं होता तो मैं boys=3x and girls=2x लिखता|
Ex: In a class, the ratio of boys and girls is 3:2. If there are total 100 students, then how many boys and girls in the class.
Solution:
Let boys=3x and girls=2x
Now,
5x=100
x=20
so,boys=3x=3×20=60and girls=2x=2×20=40
Another way:
In 5 (i.e 3+2=5) students there are 3 boys
so, 1 student, there are 3/5 boys
∴ In 100 student boys are=(3/5)×100=60 boys
In 5 (i.e 3+2=5) students there are 2 girls
so, 1 student, there are 2/5 girls
∴ In 100 student girls are=(2/5)×100=40 girls
OR
girls=100-60=40 girls
Shortcut:
boys=(3/5)×100=60 boys
Girls=(2/5)×100=40 girls
Important Point:
⇒ For a ratio, the two quantities must be in the same unit.
Ex: Ratio of Rs 5 to Rs 30 here unit=Rs. In this example both quantities unit are same.
So, Ratio=5/30=1:6
Ex-2 Ratio of Rs 5 to 30 paise.
Solution: we can’t express in the form of a ratio. because a unit of both quantities is not same.
if u want to express in the form of a ratio, first of all, make the unit of both quantities are same ie. Rs 5 to Rs 0.30 or 500 paise to 30 paise.
Rule:
The multiplication or division of each term of a ratio by the same non-zero number does not effect the ratio.
Ex: 4:5

PROPORTION:
If the ratio of the first and second quantities is equal to the ratio of the third and fourth quantities then it is called proportion.
It is represented by → ‘::’
i.e if a:b=c:d, we write a:b::c:d and we say that a, b, c, d are in proportional
Here a and d are called extremes while b and c are called mean terms.
Ex: check 6, 10, 48, 80 are in proportional
Solution: 6/10=3/5=3:5
and 48/80=3/5=3:5
so, 6, 10, 48, 80 are in proportional.
⇒ Fourth Proportional: If a:b=c:d, then d is called the fourth proportional to a, b, c.
⇒Fourth Proportional(d) =(b×c)/a
⇒ Third Proportional: If a:b=b:c, then c is called the third proportional to a and b.
⇒Third Proportional(c)=b²/a
⇒Mean Proportional between a and b= √ab.
⇒Duplicate ratio of a:b= a²:b² .
⇒Sub-duplicate ratio of a:b= √a:√b .
⇒Triplicate ratio of a:b = a³:b³
A common type of Ratio And Proportion problem that is frequently asked in the various competitive exam.
(Q1)If A:B=2:3 B:C=4:3 Find A:B:C
Solution:
[Concept: A:B and B:C दोनों में B common है so दोनों में जो B का ratio दिया हुआ है उसे equal करेंगें|]
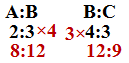
∴ A:B:C=8:12:9 Ans.
2nd Method:
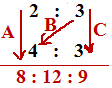
∴ A:B:C=8:12:9 Ans.
(Q2) A:B=2:1 and A:C=1:3 then A:B:C is
Solution:
[Concept: A:B and A:C दोनों में A common है so दोनों में जो A का ratio दिया हुआ है उसे equal करेंगें|]
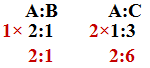
∴ A:B:C=2:1:6 Ans.
(Q3)If A:B=5:2 B:C=2:3 C:D=5:3 find ratio of A:B:C:D=?
Solution:

[Concept: A:B:C and C:D दोनों में C common है so दोनों में जो C का ratio दिया हुआ है उसे equal करने के लिए 5 से multiply किया गया है|]
(Q4)If A:B=4:9 and A:C=2:3 then (A+B):(A+C) is.
Solution:
[Concept: A:B and A:C दोनों में A common है so दोनों में जो A का ratio दिया हुआ है उसे equal करेंगें|]

∴ A:B:C=4:9:6
Now,
(A+B):(A+C)=(4+9):(4+6)=13:10 Ans.
(Q5)If 2A=3B=4C, then A:B:C is.
Solution:
L.C.M of 2,3,4=12
Now,
2A/12 =3B/12 = 4C/12
A/6 = B/4 = C/3
A:B:C=6:4:3 Ans.
(Q6)If A=(1/4)B and B=(½)C then A:B:C is
Solution:
A/B=1/4 and B/C=1/2
A:B=1:4 and B:C=1:2
[Concept: A:B and B:C दोनों में B common है so दोनों में जो B का ratio दिया हुआ है उसे equal करेंगें|]

So, A:B:C=1:4:8 Ans.
(Q7)If A:B=2:3 and B:C=3:7 then (A+B):(B+C):(C+A) is.
Solution:
[Concept: A:B=2:3 B:C=3:7 दोनों में B common है so दोनों में जो B का ratio दिया हुआ है उसे equal करेंगें| but in this question ratio of B in both cases are equal.]
∴ A:B:C=2:3:7
So, (A+B):(B+C):(C+A)=5:10:9 Ans.
(Q8)If x:y=4:5 then (3x+4y):(5x+3y)=?
Solution:
x:y=4:5
x/y=4/5
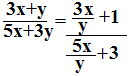
Put the value of x/y then
(3x+4y):(5x+3y)=17:35 Ans.
(Q9)If a:b:c=2:3:4 and 2a-3b+4c=33, then the value of c is.
Solution:
a:b:c=2:3:4
∴ a/2 = b/3 = c/4 = K(let)
⇒ a=2k, b=3k, and c=4k
Given that 2a-3b+4c=33
=>2×2k-3×3k+4×4k=33
so, k=3
∴ c=4k=4×3=12 Ans.
(Q10)The fourth proportional to 4, 9, 12 is.
Solution:
Let the fourth proportional to 4, 9, 12 be x.
then 4:9::12:x
⇒4×x=9×12 (i.e a×d=b×c)
∴ x=27 Ans.
(Q11)The third proportional to 16 and 36 is.
Solution:
Let the third proportional to 16 and 36 be x
then 16:36:36:x
⇒ 16×x=36×36
∴ x=81 Ans.
(Q12)The mean proportional between 0.08 and 0.18 is.
Solution:
The mean proportional between 0.08 and 0.18=
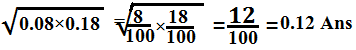
I have already shared a Time and Work, Pipe and Cistern problem Shortcut Tricks, Basic concept and frequently asked question if you have not read that yet, you should read it the right way here is the link.
Time and Work Problem Shortcut Tricks Type-1
Pipe and Cistern Problem Shortcut Tricks Type-1
If you have any queries regarding this topic fell free to ask me in the comments below.
Did you like this article? Share it with your friends on facebook, Twitter, Whatsapp and Google plus!







![[हिंदी] उच्च न्यायालय (High Court) MCQ Quiz – Objective Questions with Answer For SSC, UPPCS, IAS, CDS, BPSC, MPPCS Exam उच्च न्यायालय (High Court) MCQ Objective Questions Hindi](https://www.crackgovexam.com/wp-content/uploads/2023/10/उच्च-न्यायालय-High-Court-MCQ-Hindi-218x150.jpg)
![[हिंदी] सर्वोच्च न्यायालय/उच्चतम न्यायालय (Supreme Court) MCQ Objective Questions with Answer SSC Exam Hindi वर्ष 1999 से 2024 तक सर्वोच्च न्यायालय (Supreme Court) MCQ Objective Questions Hindi](https://www.crackgovexam.com/wp-content/uploads/2023/10/सर्वोच्च-न्यायालय-Supreme-Court-MCQ-Hindi-218x150.jpg)
![[हिंदी] मौलिक कर्त्तव्य (Fundamental Duties) MCQ Quiz – Objective Questions with Answer For SSC, UPPCS, IAS, CDS, BPSC, MPPCS Exam मौलिक कर्त्तव्य (Fundamental Duties) MCQ Objective Questions Hindi](https://www.crackgovexam.com/wp-content/uploads/2021/07/मौलिक-कर्त्तव्य-Fundamental-Duties-MCQ-Hindi-218x150.jpg)





























Ur All math tricks are the best way & best solution…..& This is definitely crack for any type of competition….!!!Ur all article are very much helpful for all….& For Me also…!!!!